About
𝕊tefano ℙeluchetti
I am research scientist at Sakana AI. Previously, I was principal research scientist at Cogent Labs, and senior quantitative analyst and data scientist at HSBC. I obtained an MSc in Economics and a PhD in statistics from Bocconi University, the latter under the supervision of Gareth O Roberts.
I conduct research in deep learning and statistics. My interests include:
- interplay between neural networks and stochastic processes;
- probabilistic numerics;
- generative modeling.
Research
Featured Topics
Generative transports
In recent years, transportation of probability measures has garnered significant interest as a computational tool for sampling. In [Pel21], we introduce the Diffusion Bridge Mixture (DBM) transport, a novel method for constructing dynamic transports between two target distributions. Broadly speaking, the approach involves: (1) mixing a diffusion bridge over its endpoints with respect to the target distributions and; (2) matching the marginal distributions of the process of step (1) through a diffusion process. This work precedes several others that develop dynamic transports, such as [LCB⁺23] and [TMH⁺23], which are shown to be closely related to the DBM transport in [SDC⁺23]. For instance, the approach by [LVH⁺23] is equivalent to the DBM transport based on a Brownian bridge, and the same settings recover the rectified flow of [LGL22] as the Brownian bridge randomness vanishes.
In [Pel23], we apply the DBM transport to generative visual applications, achieving accelerated training and superior sample quality at wider discretization intervals comparatively to the score-based generative modeling (SGM) approach of [SSK⁺21]. Additionally, we introduce the Iterated Diffusion Bridge Mixture (IDBM) procedure, which is shown to convergence toward the solution of the dynamic Schrödinger bridge problem. Contrary to the classical algorithm utilized to solve this problem, the Iterative Proportional Fitting (IPF) procedure, the IDBM procedure realizes a valid coupling between the target probability measures at each step. Furthermore, the IDBM procedure exhibits improved robustness properties, which are especially relevant when solving the dynamic Schrödinger bridge problem to approximate an optimal transport map.
Large neural networks as stochastic processes
The seminal work by [Nea96] established a connection between infinitely wide neural networks (NNs) and Gaussian processes (GPs), assuming parameters that are identically and independently distributed (iid) with finite variance. This result has significant implications, such as facilitating the analysis of the trainability of very deep NNs and the design of efficient covariance kernels for GP inference in perceptual domains. In [PFF20], [FFP23a], and [FFP23b], we investigate wide NN limits arising from iid parameters with an α-Stable distribution, characterized by heavy tails. Our convergence results are developed in the more realistic yet challenging setting of joint growth in the layers' width. These convergence findings, applicable to the prior NN model or the NN at initialization, are complemented by an analysis of the training dynamics in the Neural Tangent Kernel (NTK) regime.
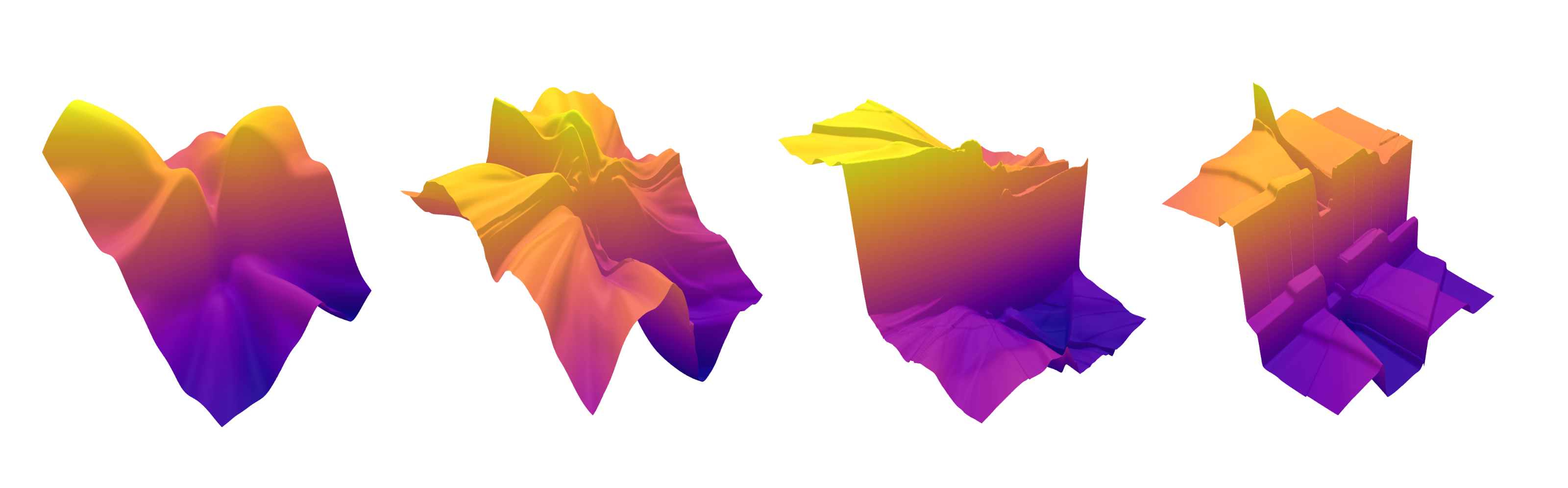
In [PF20], we initiate the study of stochastic processes associated to infinitely deep NNs. To obtain non-degenerate limits, the NN architecture must be residual with identity mapping ([HZR⁺16]). Under suitable conditions, as depth grows unbounded, convergence towards diffusion processes is achieved, assuming iid parameters with a Gaussian distribution. These findings are expanded in [PF21] to include the convolutional setting, the doubly infinite limit in depth and width, and results regarding the training dynamics in the NTK regime.
Probabilistically augmented data structures
The Count-Min Sketch (CMS, [CM05]) is a randomized data structure designed to estimate token frequencies in large data streams by using a compressed representation through random hashing. A probabilistic augmentation of the CMS is introduced in [CMA18], where, under a Dirichlet process prior on the data stream, posterior token frequencies are obtained conditionally on the random hashes' counts. However, data streams often exhibit long tails in token count frequencies, as observed in text corpora. To address this, in [DFP21] and [DFP23], we propose more suitable priors for the data stream, featuring a more flexible tail behavior. This broader approach presents significant challenges, necessitating the introduction of both novel theoretical arguments and scalable inferential procedures that accommodate the increased model complexity. In addition to providing uncertainty estimates, our Bayesian approach exhibits improved performance in estimating low-frequency tokens.
Bibliography
2023 —
2022 —
2021 —
2020 —
2019 —
2013 —
2012 —
† : alphabetically ordered — equal contribution.
Dev
SciLua
SciLua is a scientific computing framework designed for LuaJIT, focusing on a curated set of widely applicable numerical algorithms. It includes linear algebra (with optional language syntax extensions), automatic differentiation, random variate and low-discrepancy sequence generation modules. The framework also incorporates an implementation of the No-U-Turn Sampler (NUTS) from [HG14], a robust gradient-based MCMC algorithm, as well as a slightly improved version of the Self-adaptive Differential Evolution (SaDE) algorithm by [QS05], a global stochastic optimizer. All components have been meticulously optimized for peak performance. As of 2023, SciLua-LuaJIT ranks first in the Julia Micro-Benchmarks relatively to the no-checks reference C implementation, with ∼ 9% performance gap.
-- for python quants 2015 presentation
ULua
ULua is a cross-operating-system, cross-architecture, binary LuaJIT distribution. Featuring its own package manager and package specifications, ULua enables bundling dynamic libraries and endorses semantic versioning for simplified dependency resolution. A build system, utilizing multiple VMs, automatically generates binary packages from LuaRocks. Moreover, ULua is fully self-contained and relocatable, even across operating systems.
All my projects are hosted at GitHub.